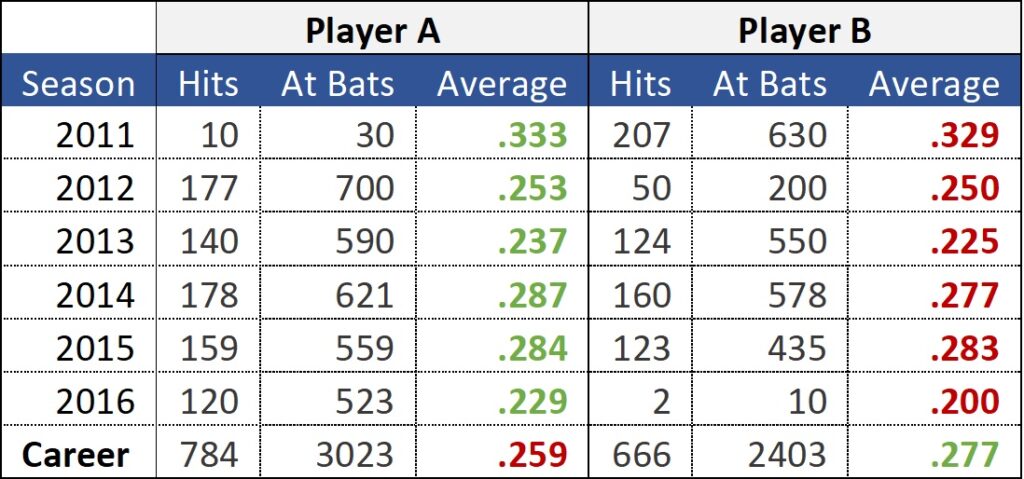
Take two baseball players. Player A has outhit Player B every season.

What if I told you that Player B has a higher career average over the 2011-2016 stretch than Player A?
Simpson’s Paradox
What’s going on here?
In statistics, this phenomenon is called “Simpson’s Paradox.” It refers to when a statistical trend observed in groups is reversed when the data is aggregated.
Revisiting the data, you can see that the number of at bats can vary dramatically between the two players for the same season.
For example, both Player A and Player B had their best season averages in 2011.
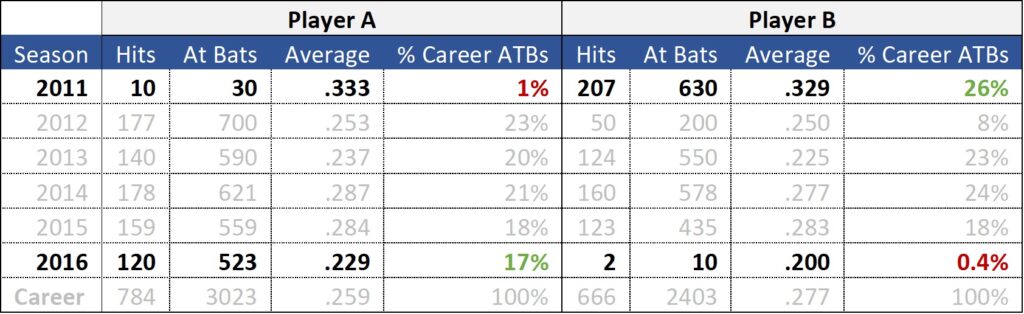
Although Player A hit .333 in 2011, he only had 30 at bats. Therefore, the .333 season, which was Player A’s best, only contributed to 1% of Player A’s career at bats.
Player B had a slightly lower average in 2011, but he had significantly more at bats. Player B hit .329 across 26% of his career at bats.
From a weighted average perspective, Player B’s best season contributed more heavily to his career average than Player A’s.
In the 2016 season, the opposite happened. Both Player A and B posted their worst batting averages. But for Player A, the 2016 season contributed to 17% of his career average. For Player B, the worst season only contributed to 0.4% of his career at bats.
The difference between at bats per season explains why Player B has a better career average than Player A, despite having a lower batting average in every season.
The Paradox in Real Life
Simpson’s Paradox has occurred between real players in the major leagues. For example, through 1995 and 1996, David Justice had a higher average in both seasons than Derek Jeter, but Derek Jeter actually had a .40 higher average over the two year period.
Simpson’s paradox was also observed in an accusation of gender bias against UC Berkeley. Male applicants to graduate programs were more likely to be admitted than female applicants. But when researchers calculated the rate by department, they found that most departments actually slightly favored female applicants.
It turned out that women were more likely to apply to competitive programs than men, contributing to their lower admission rate overall. In statistical terms, gender represented a confounding variable that contributed to the paradox.
Want to learn more? We recommend an article by towardsdatascience.com if you’re interested in learning more about the topic. Or, if you’ve run across this problem in real life, let us know at [email protected]!



